Hệ số góc là gì là vấn đề thắc mắc của nhiều người. Đối với thuật ngữ này, bạn sẽ gặp nhiều trong bộ môn toán học. Đặc biệt là kiến thức toán ở cấp ba. Bạn cần hiểu rõ mới có thể tính toán đúng đắn. Trong bài viết sau, chúng ta cùng tìm hiểu thông tin cụ thể hơn về hệ số góc nhé.
Hệ số góc (angle coefficient) là một giá trị số thể hiện tỷ lệ độ dốc của đường thẳng trong một hệ tọa độ trục. Được sử dụng để xác định vị trí và tính toán trong toán học, các đặc tính của đường thẳng như độ dốc, góc giữa với trục hoành hoặc trục tung. Hệ số góc của đường thẳng được tính dẫn dắt bằng số của tỷ lệ chiều cao của điểm đó trên đường thẳng so với chiều rộng tương ứng.
Ngoài ra còn có thêm định nghĩa khác đưa ra giải thích hệ số góc là gì. Tại mặt phẳng của hệ trục tọa độ Oxy thì hệ số góc một đường thẳng (d) xác định là tan α. α chính là góc tạo bởi đường thẳng (d) với chiều dương trục Ox. Ta sẽ gặp một số trường hợp dưới đây:
Mệnh đề 1: Dạng y = ax + b là phương trình đường thẳng (d) với hệ số góc là a.
Mệnh đề 2: Dạng y = a (x-x0)+y0. Phương trình tạo nên bởi đường thẳng (d) qua điểm M0 (x0;y0), hệ số góc a.
Hai đường thẳng song song hoặc trùng nhau có cùng hệ số góc.
Hiểu thêm: Tỉ Lệ Thức là gì? Tìm hiểu các tính chất toán học của tỷ lệ thức
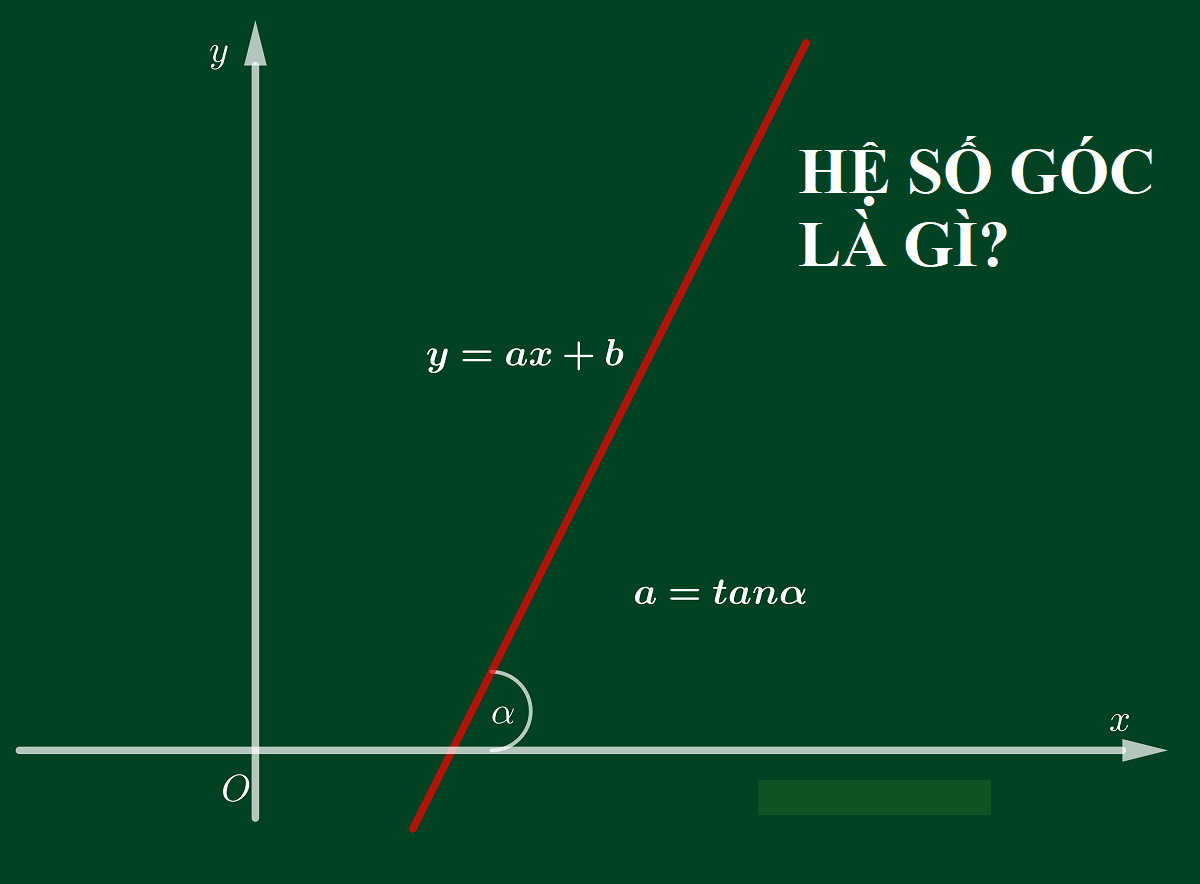
Sau khi hiểu sơ lược về khái niệm hệ số góc là gì, chúng ta xét hệ số góc với những đường thẳng gồm y = ax + b, tiếp tuyến và hệ số góc k.
Theo quy định thì hệ số k phụ thuộc mặt phẳng Oxy và đường thẳng đã cho. Tùy từng dữ liệu đề bài đưa ra, chúng ta thay lần lượt các dữ liệu vào đường thẳng a. Từ đó tìm ra thông tin hệ số góc k. Cuối cùng kết quả bạn tìm được sẽ là hệ số góc k.
Đối với trường hợp này, đề bài ra dữ liệu tiếp tuyến có đồ thị hàm số ở một điểm mà hoành độ x = a. Muốn tính hệ số góc tiếp tuyến, chúng ta cần thực hiện theo những bước dưới đây:
Nếu muốn tính hệ số góc là gì của mặt phẳng Oxy với đường thẳng y = ax + b, ta xét những trường hợp sau:
Hệ số a lúc này chính là hệ số góc của mặt phẳng Oxy với đường thẳng y = ax + b.
Đọc thêm: Phương pháp, cách nhân chia số Hữu Tỉ sao cho đúng
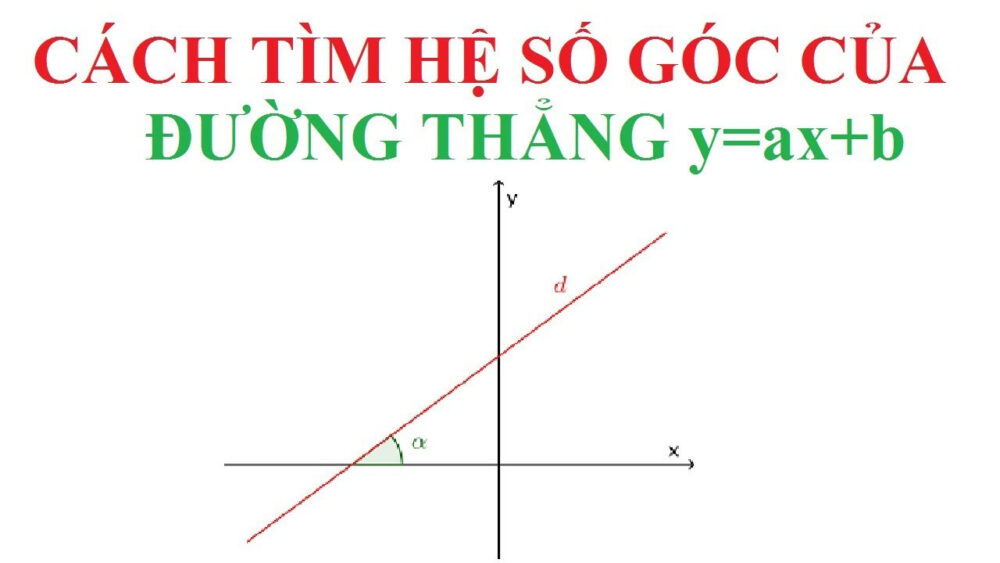
Đường thẳng d bất kỳ thường viết công thức tổng quát ở dạng Ax + By + C = 0 (B ≠ 0). Lúc này, ta chuyển hệ số góc đường thẳng d sang dạng hệ số góc đường thẳng là y = ax + b. Ta có phương trình A/Bx + y + C/B=0, dẫn đến y = – A/Bx – C/B. Trong trường hợp này, hệ số góc đường thẳng d ta cần tìm đó là k = -A/B.
Ví dụ 1: Cho hàm số y = x + 2. Bạn đi tìm góc tạo bởi trục Ox (làm tròn tới phút) và đường thẳng y = x + 2. Mẫu gợi ý như sau:
Ví dụ 2: Cho (d): y = ax + b. Bạn đi tìm a, b biết (d) song song với (d’) và đi qua gốc tọa độ. Trong đó hệ số góc của (d’) bằng 1. Gợi ý về đáp án như sau:
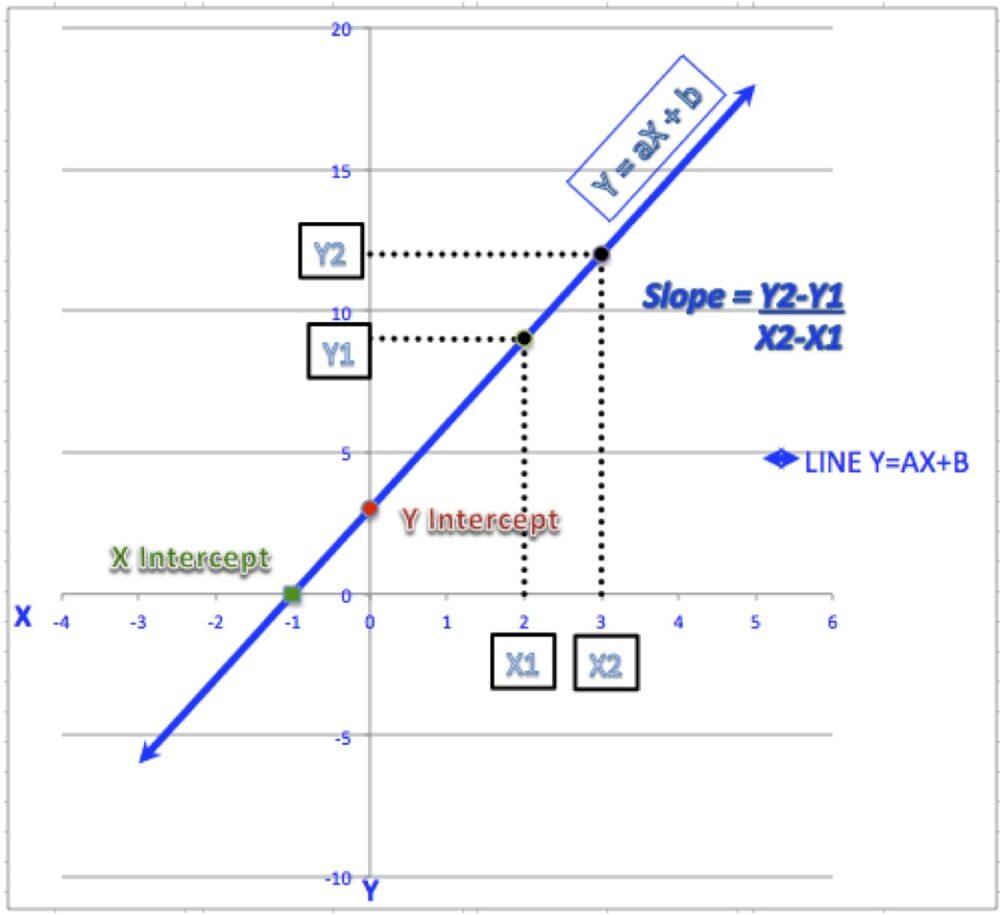
Thông tin hệ số góc là gì đã có thông tin ở trên. Ligru mong là những chia sẻ này sẽ giúp bạn hiểu rõ khái niệm, nắm được cách tính toán hệ số góc trong toán học.
Bài viết liên quan
Violym là gì? Tìm hiểu chi tiết về Violympic tại Việt Nam
Ngày nay, học sinh đến trường bên cạnh những giờ học chính khóa, các em có rất nhiều cơ...

Toán Soroban là gì? Có nên cho các con học toán Soroban?
Toán soroban là gì? Nên cho các con học toán soroban không? Trẻ từ mấy tuổi có thể học...
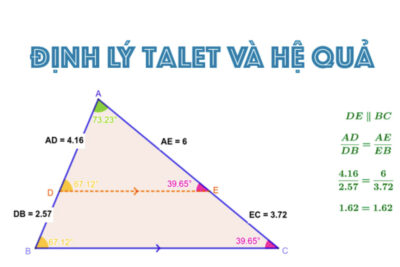
Định lý Ta lét trong toán học, công thức và hướng dẫn cách tính
Trong lĩnh vực Toán học, định lý Ta lét là một kiến thức vô cùng quan trọng, được đem...
Phương pháp, cách nhân chia số Hữu Tỉ sao cho đúng
Kiến thức toán học liên quan đến vấn đề nhân chia số hữu tỉ đã và đang được rất...

Toán Rời Rạc là gì? Giải đáp một số thông tin về Toán Rời Rạc
Toán rời rạc là bộ môn khó nhưng được nhiều người đánh giá hay và rèn luyện tư duy...
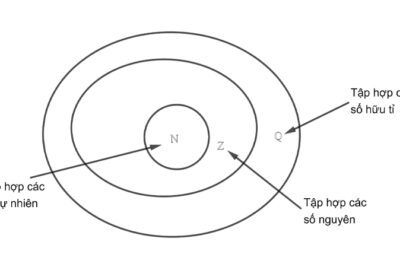
Tập hợp Q và tất tần tật những điều thú vị nên biết
Tập hợp Q là dạng bài tập thường xuyên xuất hiện trong toán học trung học cơ sở. Tuy...