Trong lĩnh vực Toán học, định lý Ta lét là một kiến thức vô cùng quan trọng, được đem vào các chương trình học từ cấp bậc trung học. Trong bài viết dưới đây chia sẻ nội dung về định lý Talet cho bạn đọc cập nhật thêm được những thông tin quan trọng trong bộ môn toán học. Cùng theo dõi nhé.
Định lý Ta lét hay còn được gọi là định lý Thales, nó đóng vai trò rất quan trọng trong lĩnh vực hình học nói riêng và Toán học nói chung. Định lý này được đặt theo tên của nhà Toán học Thales đến từ Hy Lạp.
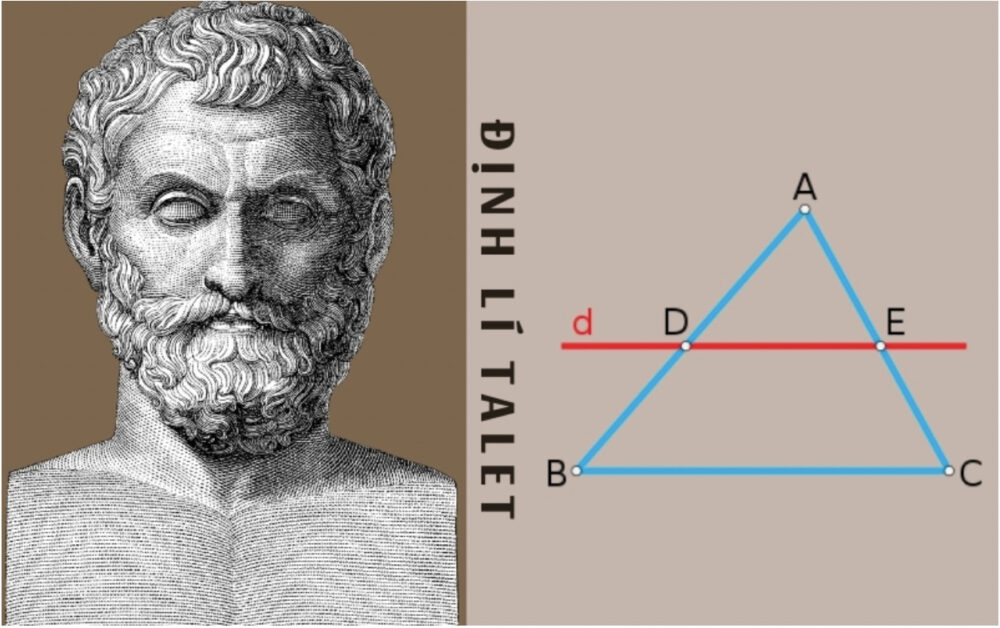
Định lý Talet trong tam giác được phát biểu như sau: khi có 1 đường thẳng song song với 1 cạnh của tam giác và đồng thời cắt 2 cạnh còn lại thì sẽ định ra trên 2 cạnh được cắt bởi đường thẳng đó thành những đoạn thẳng có tỷ lệ tương ứng nhau. Để giúp bạn hiểu rõ hơn về định lý này, bạn có thể tham khảo qua ví dụ sau:
Trong △ABC có đoạn thẳng BC// B’C’ thì ta sẽ có định lý Talet như sau:
Định lý Talet đảo sẽ được phát biểu như sau: nếu một đường thẳng cắt hai cạnh của một tam giác và chia ra trên hai cạnh này thành những đoạn thẳng tương ứng tỉ lệ bằng nhau thì đường thẳng đó song song với cạnh còn lại của tam giác. Một lưu ý quan trọng của định lý Ta lét đảo vẫn được áp dụng trong trường hợp đường thẳng cắt phần kéo dài tại hai cạnh của tam giác.
Đọc và tìm hiểu thêm: Phương pháp, cách nhân chia số Hữu Tỉ sao cho đúng
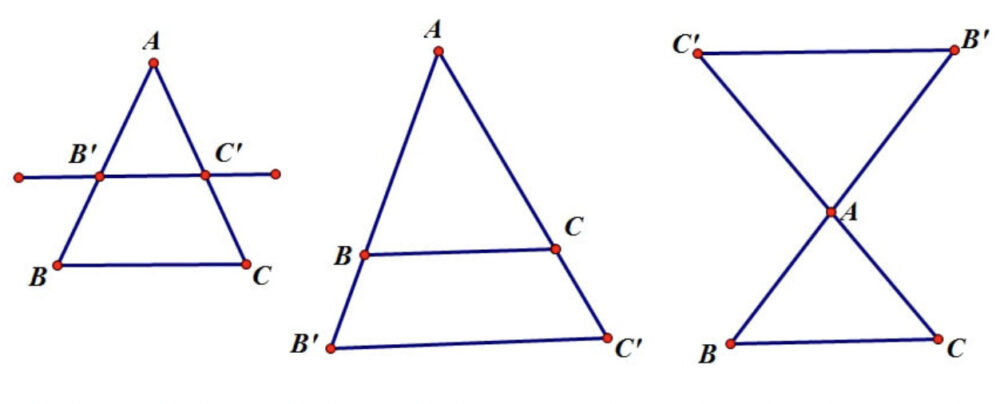
Với định lý Talet sẽ có những hệ quả như sau:
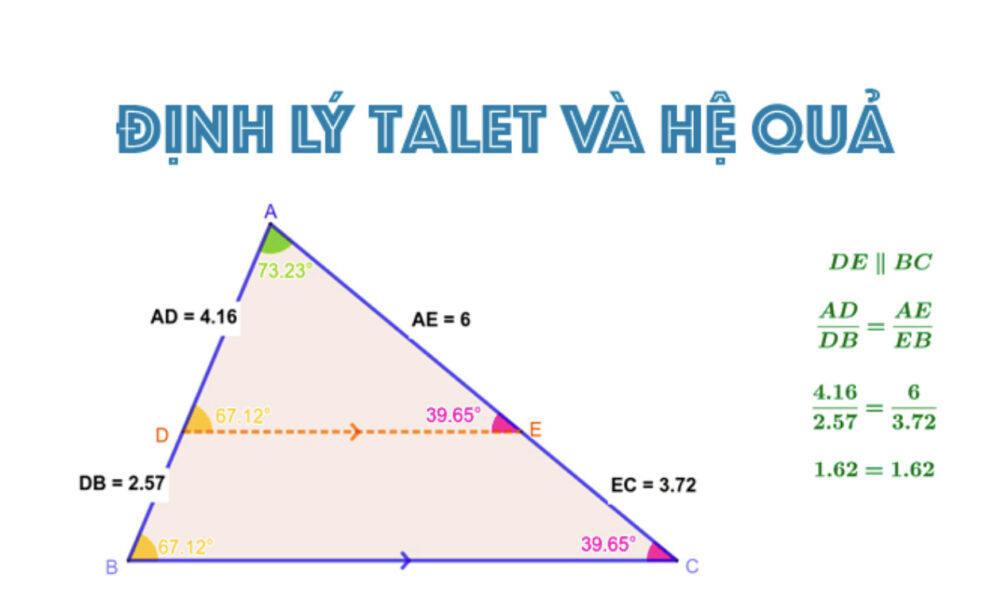
Hệ quả đầu tiên của định lý Talet được phát biểu cụ thể như sau: trong một tam giác, khi có một đường thẳng song song với một cạnh và đồng thời cắt 2 cạnh còn lại sẽ tạo ra một tam giác mới với ba cạnh có tỷ lệ tương ứng với ba cạnh của tam giác cho trước.
Trong △ABC có đường thẳng DE // BC thì ta sẽ có:
Đặc biệt, hệ quả 1 vẫn đúng với trường hợp như sau: khi có một đường thẳng a song song với 1 cạnh bất kỳ của tam giác đã cho và cắt 2 cạnh còn lại của tam giác khi kéo dài thì 3 cạnh của tam giác mới vẫn có tỷ lệ tương ứng 3 cạnh của tam giác trước đó.
Hệ quả 2 của định lý Ta lét trong tam giác được phát biểu như sau: Khi một đường thẳng cắt ngang 2 cạnh của một tam giác đã cho từ trước đồng thời song song với cạnh còn lại thì sẽ tạo được 1 tam giác mới đồng dạng với tam giác đã cho trước.
Định lý Talet trong tam giác với hệ quả 3 được phát biểu như sau: Khi ba đường thẳng đồng quy thì sẽ chắn trên 2 đường thẳng song song những cặp đoạn thẳng tỉ lệ với nhau. Hệ quả này được xem là một định lý Ta lét mở rộng trong bộ môn Toán học.
Đọc và tìm hiểu thêm: Tỉ Lệ Thức là gì? Tìm hiểu các tính chất toán học của tỷ lệ thức
Bên cạnh định lý Ta lét tam giác nêu trên thì bạn có thể áp dụng định lý Talet trong hình thang. Theo đó, định lý này trong hình thang được phát biểu như sau: trong một hình thang nếu có một đường thẳng song song cùng 2 cạnh đáy đồng thời cắt 2 cạnh bên hình thang đó thì sẽ tạo thành 2 cạnh bên những đoạn thẳng có tỷ lệ tương ứng nhau.
Định lý Ta lét không chỉ được ứng dụng trong hình học phẳng mà nó còn được ứng dụng trong hình học không gian. Theo đó, định lý Talet trong không gian được phát biểu như sau: khi có 3 mặt phẳng song song trong không gian sẽ chắn trên 2 đường thẳng tạo thành những đoạn thẳng có tỷ lệ tương ứng nhau.
Trên đây là bài viết Ligru chia sẻ các kiến thức về định lý Ta lét trong bộ môn Toán học. Mong rằng qua những nội dung đó đã giúp bạn hiểu hơn về định lý này và áp dụng thành công.
Bài viết liên quan

Toán Rời Rạc là gì? Giải đáp một số thông tin về Toán Rời Rạc
Toán rời rạc là bộ môn khó nhưng được nhiều người đánh giá hay và rèn luyện tư duy...

Hệ số góc là gì, lý thuyết hệ số góc của đường thẳng y=ax+b
Hệ số góc là gì là vấn đề thắc mắc của nhiều người. Đối với thuật ngữ này, bạn...
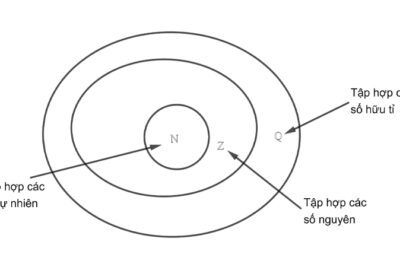
Tập hợp Q và tất tần tật những điều thú vị nên biết
Tập hợp Q là dạng bài tập thường xuyên xuất hiện trong toán học trung học cơ sở. Tuy...

Công thức tìm X tiểu học là gì? Hướng dẫn cách ghi nhớ nhanh
Công thức tìm X là gì luôn là chủ đề được rất nhiều người quan tâm, đặc biệt là...
Phương pháp, cách nhân chia số Hữu Tỉ sao cho đúng
Kiến thức toán học liên quan đến vấn đề nhân chia số hữu tỉ đã và đang được rất...

Tìm hiểu các Quy Tắc Giải Toán Tìm X lớp 3 nâng cao
Bài toán tìm x lớp 3 có những quy tắc nào? Đây là câu hỏi được rất nhiều em...