Tập hợp Q là dạng bài tập thường xuyên xuất hiện trong toán học trung học cơ sở. Tuy nhiên, không phải học sinh nào cũng học tốt những bài học về tập Q. Bật mí ngay những điều vô cùng thú vị về tập số này, từ đó giúp cho các bạn học sinh hứng thú hơn khi giải bài tập về tập số hữu tỉ – Q.
Tập hợp Q là tập hợp tất cả những số hữu tỉ có thể biểu diễn dưới dạng phân số a/b trong đó:
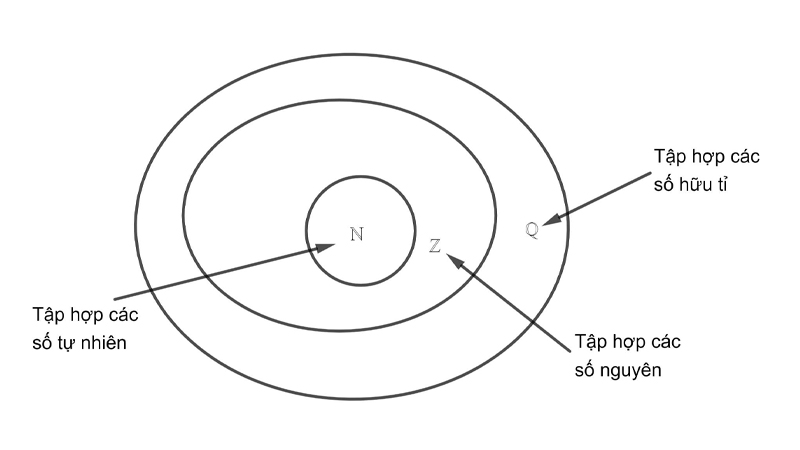
Như vậy, tập số Q là một trong những tập số rộng, xét về mối quan hệ giữa các số, Q bao hàm những tập hợp sau:
Khi nói về tập hợp Q – tập hợp những số hữu tỉ, ta cần biểu diễn được những số này trên trục số. Thông thường, cách để biểu diễn các số hữu tỉ trên trục số không khó nếu tuân theo các bước sau đây:
Chúng ta cần tiến hành chia đoạn [0,1] trên trục số thành b phần bằng nhau, ta sẽ có đơn vị mới được xác lập là 1/b để biểu diễn số hữu tỉ a/b thuộc tập hợp Q.
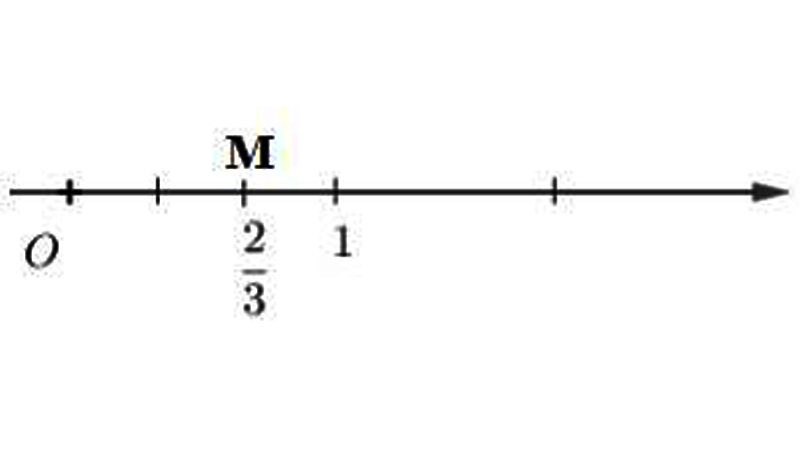
Đến bước này, số lần a hoặc |a| đếm được và chấm trên trục số được gọi là điểm a/b hay điểm biểu diễn số hữu tỉ a/b thuộc tập hợp Q.
Mỗi một số thuộc các tập hợp đều có cho mình những tính chất số học riêng của nó. Những số hữu tỉ thuộc tập hợp này sẽ có những tính chất như:
Học ngay về tính chất của các số thuộc tập Q
Chúng ta đều biết rằng mọi tập số đều có những điều thú vị xung quanh nó, tập hợp Q bao gồm những con số hữu tỉ cũng có những điều thú vị mà các bạn có thể khám phá ngay sau đây:
Việc giải những bài tập liên quan đến số hữu tỉ thuộc tập hợp này vẫn luôn là vấn đề nhận được sự quan tâm của các bạn học sinh. Để có thể làm những bài tập thuộc tập hợp này các bạn cần nắm rõ:
Toàn bộ thông tin về tập hợp Q đã được gửi đến những bạn học sinh thân yêu. Việc có thể giải những bài tập liên quan đến tập số này không bao giờ là khó nếu như các bạn nắm chắc những thông tin về tập số này. Đồng thời, đừng ngại ngần hỏi thêm giáo viên để có thể làm bài tập một cách chính xác nhé.
Bài viết liên quan
Dư Giả hay Dư Dả – Từ nào viết đúng trong Tiếng Việt?
Nhiều người hiện nay thắc mắc trong việc sử dụng từ dư giả hay dư giả? Từ nào đang...
Công thức tìm X tiểu học là gì? Hướng dẫn cách ghi nhớ nhanh
Công thức tìm X là gì luôn là chủ đề được rất nhiều người quan tâm, đặc biệt là...
Cổ Súy hay Cổ Xúy – Cách dùng từ đúng trong tiếng Việt
Cổ súy hay cổ xúy là cách sử dụng từ đúng hiện nay? Từ nay mang ý nghĩa tích...
Tỉnh rộng nhất Việt Nam là tỉnh nào? – Giải đáp địa lý Việt
Tỉnh rộng nhất Việt Nam là tỉnh nào? Tỉnh này có những đặc điểm gì? Lịch sử phát triển...
Tỉnh ít dân nhất Việt Nam là tỉnh nào?
Tỉnh ít dân nhất Việt Nam là tỉnh nào? Nếu bạn băn khoăn mà không biết tỉnh thành nào...
![[Giải Đáp] Sắc Xảo hay Sắc Sảo – Nên dùng từ nào cho đúng?](https://ligru.com/wp-content/uploads/2023/01/sac-sao-la-gi-400x267.jpg)
[Giải Đáp] Sắc Xảo hay Sắc Sảo – Nên dùng từ nào cho đúng?
Sắc xảo hay sắc sảo là từ đúng trong tiếng Việt? Từ này là loại từ loại gì, danh...
